Geohash est un système de géocodage des coordonnées géographiques (latitude / longitude) inventé par Gustavo Niemeyer lors de l’écriture du site geohash.org, et mis dans le domaine public. Le système est basé sur une fonction de hachage qui subdivise la surface terrestre selon une grille hiérarchique.

Dans la vie d’un développeur, bien souvent on doit prendre en main des algorithmes afin de nous aider dans la conception de nos logiciels. Le système de geohash fait partie de ces algorithmes, qui sont à la fois simples mais élégants ! Le genre qui vous fait aimer la programmation, vous allez voir pourquoi !

Présentation de l’algorithme de geohash

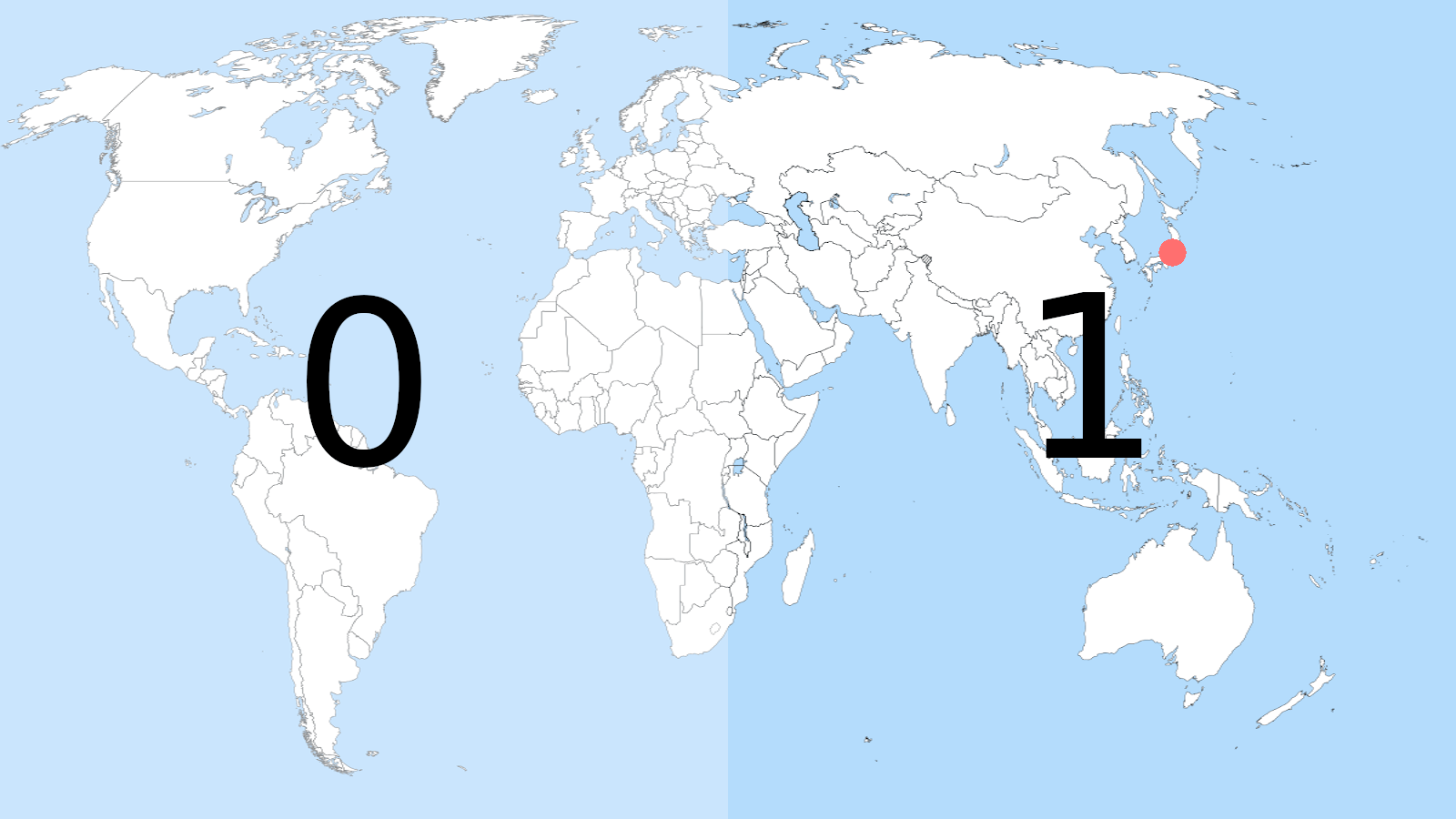
Prenons une position sur une carte (notre beau point rouge), le but de l’algorithme va être de représenter cette position comme un tag (une chaine unique). On commence par diviser la carte du monde en deux grâce à une ligne verticale et on associe à chaque moitié une valeur binaire 0 ou 1. Notre point se situe à droite dans la partie « 1 ».

On pourrait alors partager la position à quelqu’un en lui disant de nous rejoindre au Geohash « 1 » mais comme vous l’aurez facilement observé, on donnerait une indication vraiment bien imprécise, « rejoins-moi dans la moitié est de la planète ». Notre ami mettrait un temps fou à nous retrouver et pourrait potentiellement pester contre nous :D.

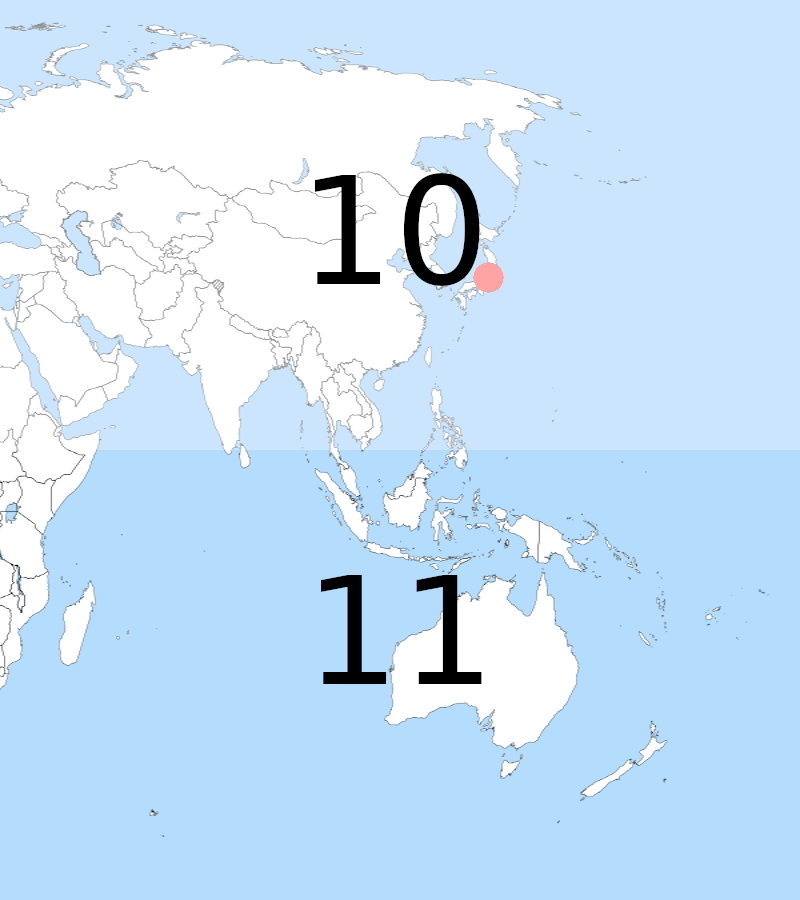
Mais rassurez-vous, on peut facilement faire mieux, il suffit d’améliorer la résolution du geohash, en scindant à nouveau la partie « 1 », mais cette fois-ci avec une division horizontale et on assigne cette fois « 0 » en haut et « 1 » en bas. On obtient ceci :

On avance, on a doublé les chances que notre ami nous retrouve et on voit qu’on arrive à savoir dans quel continent on va se rejoindre ! Continuons, on divise à nouveau le résultat en deux, de manière verticale cette fois-ci.

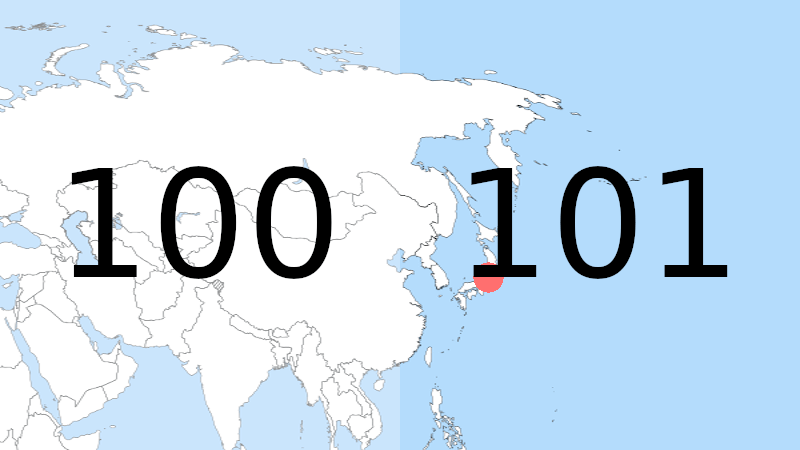
Notre geohash vaut maintenant « 101 » et on a encore gagné en précision. Vous aurez sans doute noté qu’entre chaque sous-division on alterne entre une division verticale et horizontale. Cela va permettre d’entrelacer les informations de longitude et de latitude pour ne donner qu’une seule valeur. On va continuer cet ensemble de divisions jusqu’à obtenir une précision du niveau d’une rue, voire même au-delà.

Exemple de résultat de l’algorithme de geohash

À la fin l’algorithme, notre tag sera un plus long et ressemblera surement à quelque chose comme ceci : 0010110101011100011000110001101111000111. Or, ce binaire peut être représenté sous forme de caractères alphanumériques (codés sur 32 bits). Tous les 5 bits, l’algorithme va convertir la valeur binaire en un caractère correspondant. Ce qui nous donne alors une chaîne de caractères de cette forme-là : « 5pf666y7 ».

C’est génial ton truc, mais en quoi cela nous aide-t-il?

Intérêt de l’algorithme

Voici, donc les utilisations principales de notre super tag :

• On peut l’utiliser, comme un identifiant unique: un geohash étant court et concis (au maximum, il fera 12 caractères). Ainsi, on peut facilement partager une position sur les réseaux sociaux.
• Cela peut permettre de réaliser un système de cache à échelle. Au lieu d’avoir à stocker ce qu’on appelle une bounding box (un rectangle défini par deux positions: en haut à gauche et en bas à droite), nous n’avons qu’une chaine a stocker. Grâce à ça, on peut facilement utiliser des bases de données clés-valeurs comme MongoDB, Cassandra, Memcached et j’en passe, afin de stocker et récupérer rapidement toutes les informations d’une grille donnée.
• Enfin, les geohashs permettent facilement de trouver les points les plus proches d’un lieu donné. En effet, comme les geohashs sont stockés dans un ordre alphanumérique. Cela signifie donc que les points les plus proches sont les chaînes les plus proches. Ainsi par exemple :
  • 5pf666y <-- Notre position
  • 5pf665b <-- Quelqu'un pas si éloigné de nous
  • 22rt841 <-- Position lointaine

Un petite apparté à propos de l’équivalence entre la longueur du hash et sa précision :

Longueur du geohash	Lat bits	Lng bits	Erreur lat	Erreur lng	Erreur en km
1	2	3	±23	±23	±2500
2	5	5	±2.8	±5.6	±630
3	7	8	±0.7	±0.7	±78
4	10	10	±0.087	±0.18	±20
5	12	13	±0.022	±0.022	±2.4
6	15	15	±0.0027	±0.0055	±0.61
7	17	18	±0.00068	±0.00068	±0.076
8	20	20	±0.000085	±0.00017	±0.019

Limitations du geohash

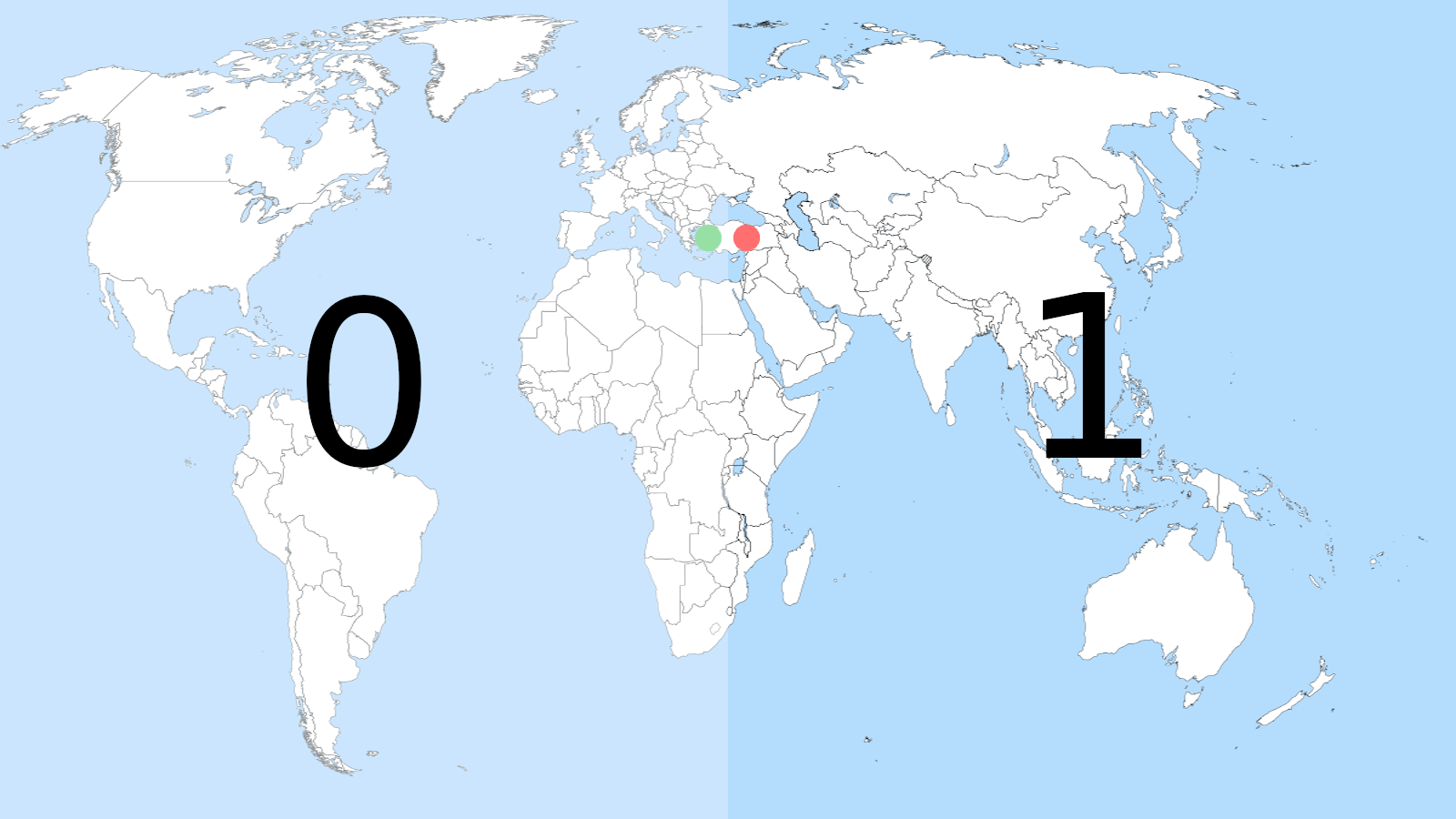
On a parlé précédemment de la recherche de points situés à proximité les uns des autres mais dans ce cas précis, les tags de geohash ont un gros défaut ! Si vous regardez bien les schémas du début, on a des cas-limites, à savoir les frontières en effet, on peut avoir des adresses très proches qui vont avoir des geohashs totalement différents. Comme sur le schéma ci-dessous :

Ici, les valeurs binaires vont être totalement opposées. Ce qui entraine forcément une corrélation très faible entre le tag final obtenu et les deux points voisins. Il existe bien évidemment une solution, Un algorithme qui va calculer la valeur des geohash des huit carrés entourant notre centre dans toutes les directions. Ce qui va permettre de récupérer également les points voisins d’une frontière.

Encodage d’une position

Nous avons vu l’idée du fonctionnement de l’algorithme, passons maintenant a une partie plus technique. L’idée du geohashing, c’est la sauvegarde par intermédiaire du résultat de deux recherches binaires. Regardons ça de plus près :

private static final int MAX_BIT_PRECISION = 64;
private static final int MAX_GEOHASH_CHARACTER_PRECISION = 12;
private static final int[] BITS = { 16, 8, 4, 2, 1 };
private static final int BASE32_BITS = 5;

public static String getGeohash(Location location, int numberOfCharacters) {
	int desiredPrecision = getDesiredPrecsion(numberOfCharacters);
	GeoHash geohash = new GeoHash();

	boolean isEvenBit = true;
	double[] latitudeRange = { -90, 90 };
	double[] longitudeRange = { -180, 180 };

	while (geohash.getSignificantBits() < desiredPrecision) {
		if (isEvenBit) {
			divideRangeEncode(geohash, longitudeRange, location.lng());
		} else {
			divideRangeEncode(geohash, latitudeRange, location.lat());
		}
		isEvenBit = !isEvenBit;
	}

	geohash.leftShift(MAX_BIT_PRECISION - desiredPrecision);
	return geohash.toBase32();
}

private static int getDesiredPrecsion(int numberOfCharacters) {
	if (numberOfCharacters > MAX_GEOHASH_CHARACTER_PRECISION) {
		throw new IllegalArgumentException("A geohash can only be " + MAX_GEOHASH_CHARACTER_PRECISION + " character long.");
	}
	int desiredPrecision = 60;
	if (numberOfCharacters * 5 <= 60) {
		desiredPrecision = numberOfCharacters * 5;
	}
	return desiredPrecision = Math.min(desiredPrecision, MAX_BIT_PRECISION);
}

private static void divideRangeEncode(GeoHash geohash, double[] range, double value) {
	double mid = (range[0] + range[1]) / 2;
	if (value >= mid) {
		geohash.addOnBitToEnd();
		range[0] = mid;
	} else {
		geohash.addOffBitToEnd();
		range[1] = mid;
	}
}

public String toBase32() {
	if (significantBits % 5 != 0) {
		throw new IllegalStateException("Cannot convert a geohash to base32 if the precision is not a multiple of 5.");
	}
	StringBuilder buf = new StringBuilder();
	long firstFiveBitsMask = 0xf800000000000000l;
	int numberOfCharacters = (int) Math.ceil(((double) significantBits / 5));
	for (int i = 0; i < numberOfCharacters; i++) {
		int pointer = (int) ((bits & firstFiveBitsMask) >>> 59);
		buf.append(Constants.BASE32[pointer]);
		bits <<= 5;
	}
	return buf.toString();
}

D’abord, on choisit la taille du geohash désiré. Puis, on vérifie que cette taille ne dépasse pas 12 caractères (le nombre maximum de bits disponible). Ici, j’utilise une classe Geohash qui va nous permettre de stocker l’avancement de l’encodage (une variable bits) et la taille de ce dernier (significantBits). Tant que notre nombre de bits, n’est pas égal à la précision désirée on continue l’algorithme.

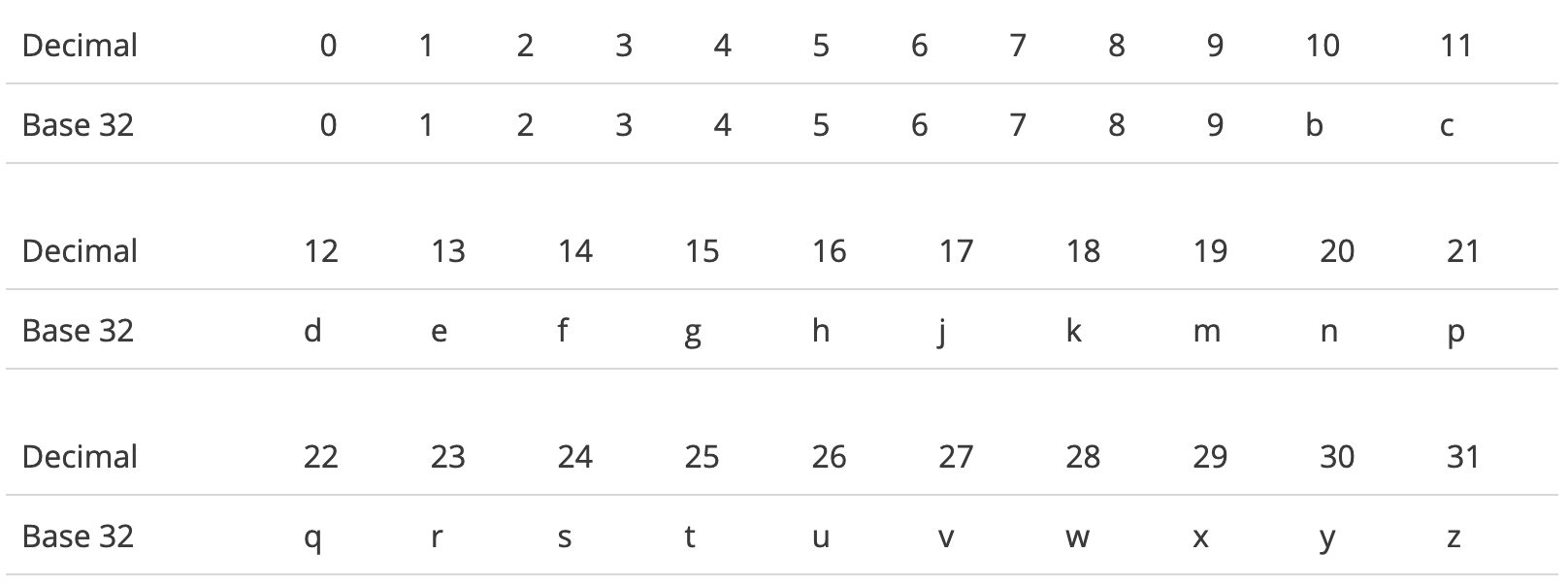
Au départ, on possède deux intervalles de référence: un pour la latitude (compris entre -90:90) et un pour la longitude (-180:180) On commence l’encodage par la longitude avec les bits pairs et on encode la latitude avec les bits impairs, à chaque tour, on va alterner. Pour chaque tour de boucle, on va augmenter ou réduire chaque range, en fonction de la valeur de la coordonnée de la position. Une fois, le tout obtenu, on va convertir les bits sous une forme de string en base 32. Attention, toutefois l’alphabet utilisé, ne contient pas les lettres suivantes: a, i, l et o.

Prenons, un exemple pour être plus clair.

Exemple d’encodage d’une position

On veut encoder la position suivante: 35.3606422, 138.7186086. Suivons l’évolution de la latitude, c’est-à-dire 35.3606422. Une latitude est toujours comprise entre -90 et 90, alors qu’une longitude est comprise entre -180 et 180.

Au premier tour de boucle, le range est donc compris entre -90 et 90. On va regarder si la valeur est supérieure ou inférieure au milieu de notre range c’est-à-dire 0. Comme c’est supérieur, on va réduire l’intervalle entre la moitié et la borne supérieure, ici: [0;90]. Dans le cas où c’est inférieur l’intervalle est réduit entre la borne inférieure et le milieu de l’intervalle. En continuant, ainsi l’algorithme, on va réussir à obtenir une précision importante.

Voici, par exemple l’intervalle obtenu après 5 passages :

desired lng: 35.3606422
current range: [-90.0;90.0]
middle interval: 0.0
new range: [0.0;90.0]
---
desired lng: 35.3606422
current range: [0.0;90.0]
middle interval: 45.0
new range: [0.0;45.0]
---
desired lng: 35.3606422
current range: [0.0;45.0]
middle interval: 22.5
new range: [22.5;45.0]
---
desired lng: 35.3606422
current range: [22.5;45.0]
middle interval: 33.75
new range: [33.75;45.0]
---
desired lng: 35.3606422
current range: [33.75;45.0]
middle interval: 39.375
new range: [33.75;39.375]

Voilà, vous devriez maintenant avoir une idée de comment encoder la position sous forme de bits.

Explication de l’algorithme de décodage d’un geohash

Pour le décodage, on va prendre l’exemple de Wikipédia qui est très clair ! On part du hash suivant: « ezs42 ». Nous allons voir comment à partir de ce hash, on va retrouver les coordonnées du lieu correspondant. Comme je vous l’ai dit pendant la phase d’encodage, on associe les bits à des caractères. Si on prend la lettre « e », par exemple, on voit que sa valeur vaut 13. Or, 13 en binaire peut s’écrire 01101 sur 5 bits. Si on décode comme ça tous le hash, on obtient les bits suivants: 01101 11111 11000 00100 00010. Comme pour l’encodage, on commence par la gauche à 0 et on alterne les bits. Ce qui nous donne, pour la longitude: 0111110000000 et pour la latitude: 101111001001.

On utilise ensuite chaque code binaire dans une série de divisions, un bit à la fois de la gauche jusqu’à la droite. On utilise toujours nos deux intervalles de départ pour la latitude (-90:90) et pour la longitude (-180:180). Si le bit est à 1, on va adapter notre intervalle à la valeur supérieure, c’est-à-dire la valeur de la moitié de l’intervalle et le maximum de l’intervalle donc par exemple pour la latitude, ça nous ferait 0:90. On répète cette procédure pour tous les bits du code.

Exemple de décodage

Pour la latitude, on part du code suivant : 101111001001. Comme le premier bit est à 1, on sait immédiatement que l’intervalle sera compris entre 0 et 90. Si on s’arrêtait ici, la latitude serait de 45, avec une erreur de ±45. En continuant de dérouler l’algorithme, on divise l’erreur et on gagne en précision. À chaque nouveau tour de boucle, l’erreur est divisée par deux.

Latitude: 101111001001

bit position	bit value	min	mid	max	mean value	maximum error
0	1	90.000	0.000	90.000	45.000	45.000
1	0	0.000	45.000	90.000	22.500	22.500
2	1	0.000	22.500	45.000	33.750	11.250
3	1	22.500	33.750	45.000	39.375	5.625
4	1	33.750	39.375	45.000	42.188	2.813
5	1	39.375	42.188	45.000	43.594	1.406
6	0	42.188	43.594	45.000	42.891	0.703
7	0	42.188	42.891	43.594	42.539	0.352
8	1	42.188	42.539	42.891	42.715	0.176
9	0	42.539	42.715	42.891	42.627	0.088
10	0	42.539	42.627	42.715	42.583	0.044
11	1	42.539	42.583	42.627	42.605	0.022

Longitude: 0111110000000

bit position	bit value	min	mid	max	mean value	maximum error
0	0	-180.000	0.000	180.000	-90.000	90.000
1	1	-180.000	-90.000	0.000	-45.000	45.000
2	1	-90.000	-45.000	0.000	-22.500	22.500
3	1	-45.000	-22.500	0.000	-11.250	11.250
4	1	-22.500	-11.250	0.000	-5.625	5.625
5	1	-11.250	-5.625	0.000	-2.813	2.813
6	0	-5.625	-2.813	0.000	-4.219	1.406
7	0	-5.625	-4.219	-2.813	-4.922	0.703
8	0	-5.625	-4.922	-4.219	-5.273	0.352
9	0	-5.625	-5.273	-4.922	-5.449	0.176
10	0	-5.625	-5.449	-5.273	-5.537	0.088
11	0	-5.625	-5.537	-5.449	-5.581	0.044
12	0	-5.625	-5.581	-5.537	-5.603	0.022

Remarque: les chiffres sont arrondis à 3 décimales pour plus de clarté.

Finalement, on retrouve la position associée au hash « ezs42 », cette dernière vaut: 42.605,-5.603. Ce qui nous amène à León en Espagne.

Décodage d’un geohash

Voici, le code correspondant à l’algorithme que je vous ai décrit :

public class Constants {
	public static final char[] BASE32 = { 
			'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 
			'b', 'c', 'd', 'e', 'f', 'g', 'h', 'j', 'k', 'm', 
			'n', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 
			'y', 'z' 
	};
	public static final byte[] BASE32_INV = new byte[(int) 'z' + 1];
	
	static {
		for (int i = 0; i < BASE32.length; i++) {
			BASE32_INV[(int) BASE32[i]] = (byte) i;
		}
	}
}

public static Location getLocation(String encodedGeohash) {
	double[] latitudeRange = { -90.0, 90.0 };
	double[] longitudeRange = { -180.0, 180.0 };

	boolean isEvenBit = true;
	GeoHash geohash = new GeoHash();

	for (int i = 0; i < encodedGeohash.length(); i++) {
		int characterToEncodeInBinary = Constants.BASE32_INV[encodedGeohash.charAt(i)];
		
		for (int j = 0; j < BASE32_BITS; j++) {
			int mask = BITS[j];
			boolean isBitActive = (characterToEncodeInBinary & mask) != 0;
			if (isEvenBit) {
				divideRangeDecode(geohash, longitudeRange, isBitActive);
			} else {
				divideRangeDecode(geohash, latitudeRange, isBitActive);
			}
			isEvenBit = !isEvenBit;
		}
	}
	
	double latitude = (latitudeRange[0] + latitudeRange[1]) / 2;
	double longitude = (longitudeRange[0] + longitudeRange[1]) / 2;

	return new Location(encodedGeohash, latitude, longitude);
}

private static void divideRangeDecode(GeoHash geohash, double[] range, boolean bitIsOn) {
	double mid = (range[0] + range[1]) / 2;
	if (bitIsOn) {
		geohash.addOnBitToEnd();
		range[0] = mid;
	} else {
		geohash.addOffBitToEnd();
		range[1] = mid;
	}
}

Utilisation du geohash pour le chargement de positions depuis une base de données

Imaginons maintenant que vous ayez une base de données dans laquelle vous assez sauvegardé un ensemble de lieux. Lors de l’insertion d’un nouveau lieu, vous pouvez calculer son geohash associé afin de pouvoir facilement lors du chargement d’un lieu récupérer les points les plus proches de ce dernier. Afin d’éviter les cas-limites dont on a discuté, il vous suffira de prendre votre lieu de départ, de trouver les voisins les plus proches. Si vous partez d’un point vous pouvez utiliser la formule d’Haversine, afin de retrouver la position la plus proche à une distance et à un degré donné. Vous pouvez trouver, un exemple dans ce gist.

Une fois que vous avez votre liste, il suffit de faire une requête SQL avec la fonction LIKE, rien de plus simple ! Par exemple :

private String buildGeoHashQuery(Location userLocation) {
    StringBuilder query = new StringBuilder("SELECT * FROM locations WHERE geohash LIKE ");
    List<Location> neighboursLocations = getUserLocationNeighbours(userLocation);
    for (Location location : neighboursLocations) {
        String currentGeoHash = GeoHashHelper.encode(location);
        query.append("'").append(currentGeoHash.substring(0, 4)).append("%' OR ").append("geohash").append(" LIKE ");
    }
    String userLocationGeoHash = GeoHashHelper.encodeBase(userLocation);
    query.append("'").append(userLocationGeoHash.substring(0, 4)).append("%;'");
    return query.toString();
}

Et c’est tout !!

Conclusion

J’espère avoir été le plus clair possible, si vous avez une demande concernant un point à éclaircir, il ne faut pas hésiter. Vous trouverez sur le repository suivant un exemple d’implémentation de cet algorithme, prêt à l’usage ;).